The purpose of options pricing is to assign a fair (theoretical) value to an option. The most famous model which is used for European style options is the Black & Scholes equations and their alternatives, whereas for the pricing of an American style option the most common model is the binomial trees.
All options pricing models are trying to capture a chaotic and unpredictable economic reality. They attempt to evaluate the price of a certain option on a certain moment of time, by using parameters which affect this price and their relations. In that sense, they are flawed mathematical representations of all the real factors that affect options prices.
Black & Scholes model
The Black & Scholes model assigns a European style option a theoretical value by using the below parameters:
1. S=current price of underline security
2. X=strike price
3. r=risk free rate
4. σ=annual standard deviation of logarithmic returns (historical volatility)
5. T=time until expiration
6. N=cumulative standard normal distribution (probability of the option to expire ITM)
The equations that describe the model are:
C is the theoretical price of the call and P is the theoretical price of the put.
Binomial trees
The valuation via binomial trees is a step by step procedure that is based on almost the same assumptions as the Black-Scholes model. It compares in every step the price of a European style option to the price that an American style option should have according to its methodology and chooses the higher of the two. American options should have a higher price than their corresponding European, because they incorporate the benefit of their early exercise.
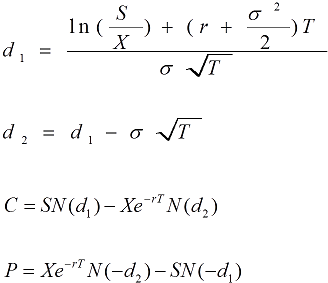
 En
En Gr
Gr