All options during their lifetime have time value, irrelevantly of their moneyness. As they approach to expiration the time value progressively diminishes and on expiration the option remains only with intrinsic value if ITM or no value at all if it is OTM. Theta measures the time value an option loses every day (including weekends and holidays), given the fact that all the other factors affecting premium remain constant. In other words it is a measure of the effects of time decay on the option premium.
Suppose we have a put (the same is applied to calls) with premium $2.30 and its Theta is 0.02. This means that every day it will be losing $0.02 in value, so if the next day all the other factors affecting the option price remain constant, it will be worth $2.28 and one day later $2.26.
Mathematically Theta is expressed by the first derivative of the option price relatively to the passage of time and its mathematical formula is:
One of its basic attributes is that it is getting bigger as expiration approaches. Many strategies which involve writing of near expiration options, attempt to take advantage of this fact in order to sell premium high and then buy it lower due to time decay.
Theta takes its highest value in ATM options because they have the highest time value and consequently more time value to lose per day. It gets smaller as options are getting more ITM or OTM because the deeper ITM or OTM an option is the less its time value.
So, if Theta is bigger when time value is bigger, we can infer that it is higher in options with many days to expiration than in options with less days to expiration and same characteristics, because the longer the option maturity the higher the possibility of being ITM and consequently the higher the time value.
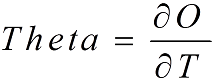
 En
En Gr
Gr