Rho measures the change of an option price which is caused by a 1% change in interest rates, given that all the other factors which affect the option price remain constant. It is not a very important parameter in options pricing because its effect is small relatively to the other factors (underline price, implied volatility, expiration).
A rise in interest rates affects positively the price of calls and negatively the price of puts. This happens because when interest rates are high then it is better for an investor to have deposited his/her money in a bank account and earning a risk free interest rate than to buy stocks. Instead he/she can control a position in stocks by buying calls which are cheaper than the outright position in stocks. This procedure raises demand for calls and accordingly their premium. On the other hand, buying puts is an indirect way to short sell stocks, but when interest rates are high, traders/investors are better off if they sell short the underline security (instead of buying puts) and earn interest on the proceeds. This decline in puts demand deflates their value.
Suppose that we have a call with premium $2.50 and Rho equals to 0.01. This means that if interest rates rise 1% the premium will rise $0.01, from $2.50 to $2.51. If we had a put with premium $2.50 and Rho 0.01 then its price would have been reduced $0.01, from $2.50 to $2.49. The opposite would have happened in a 1% decline of interest rates.
Mathematically, Rho is expressed by the first derivative of the option price relatively to a 1% rise in interest rates and its mathematical formula is:
The longer the expiration of an option the higher is its Rho. This means that in a 1% interest rates advance, calls premium rise more relatively to calls with same characteristics but closer expiration, whereas puts premium declines more than in puts with same characteristics and closer expiration.
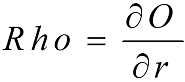
 En
En Gr
Gr